Sine meaning unveils the mathematical tapestry woven around oscillation, revealing its significance in diverse fields from physics to music. Delve into the intricacies of sine, its properties, applications, and inverse, as we embark on a journey to unravel its enigmatic allure.
Sine, a trigonometric function, stands as a cornerstone of mathematical analysis, offering a precise description of periodic phenomena that abound in nature and technology.
Sine Function: Definition, Properties, Graph, Applications, and Identities
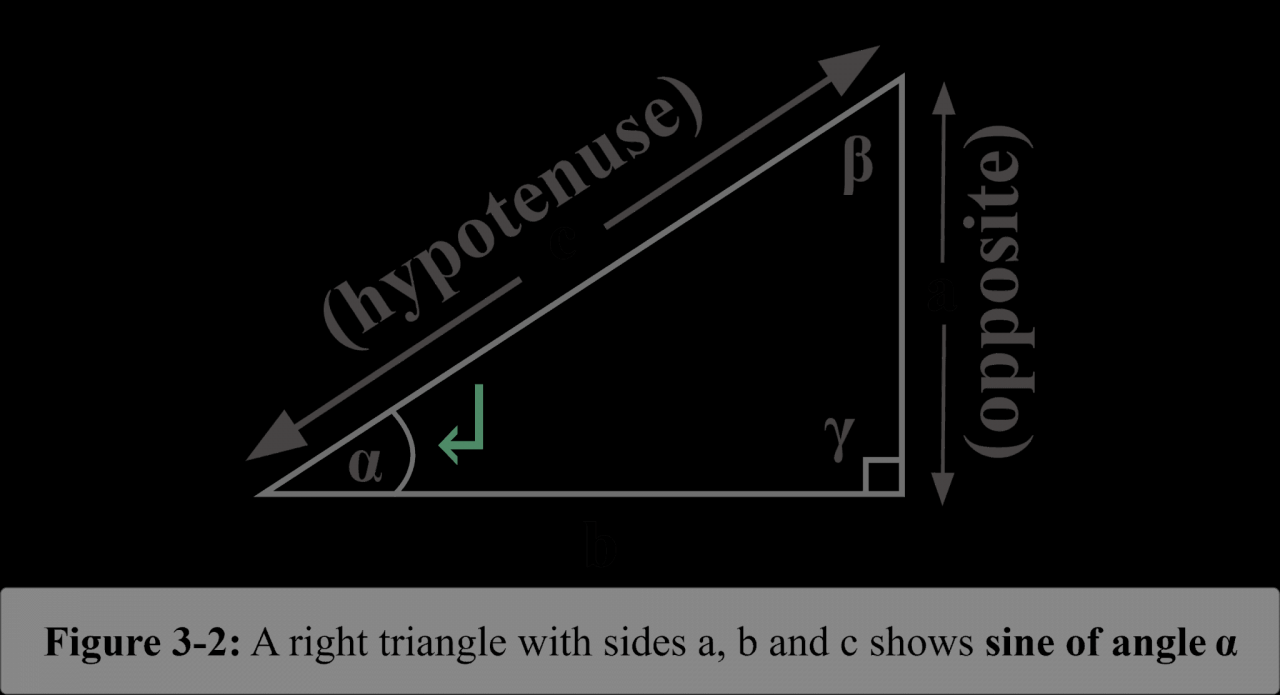
The sine function, denoted as sin(x), is a fundamental trigonometric function that describes the vertical displacement of a point moving along a unit circle. It plays a vital role in various scientific and engineering disciplines.
Definition
Mathematically, the sine of an angle x is defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right-angled triangle with an angle x.
sin(x) = Opposite side / Hypotenuse
Sine is commonly used to determine the height or vertical component of an object in a given angular position.
Properties
Sine has several key properties that define its behavior:
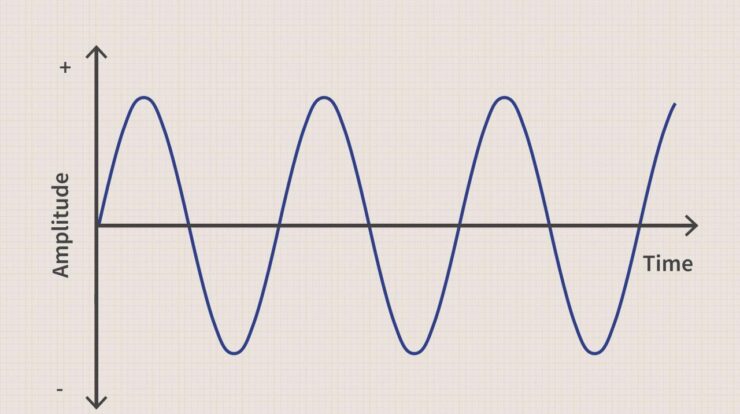
- Periodicity:Sine is a periodic function with a period of 2π. This means that it repeats its values every 2π units.
- Range:The range of sine is [-1, 1]. It oscillates between these values as the angle changes.
- Symmetry:Sine is an odd function, meaning that sin(-x) = -sin(x).
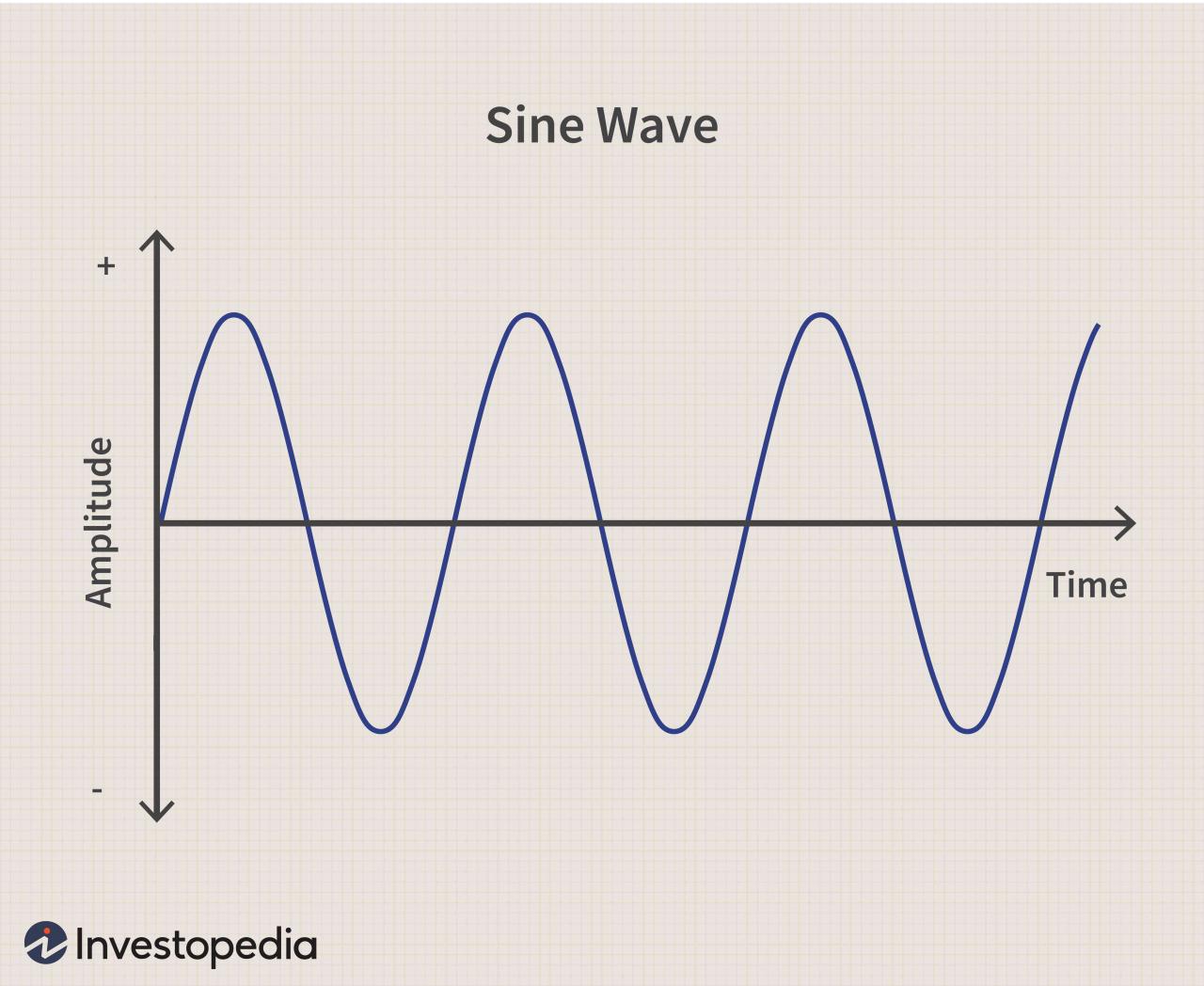
Graph
The graph of the sine function is a wave that oscillates between -1 and 1. It has a maximum value of 1 at x = π/2 + 2πn and a minimum value of -1 at x = 3π/2 + 2πn, where n is an integer.
Applications, Sine meaning
Sine has numerous applications in various fields:
- Physics:Sine is used to describe periodic motion, such as the motion of a pendulum or a vibrating string.
- Engineering:Sine is used in the analysis of AC circuits, acoustics, and structural mechanics.
- Music:Sine waves are the building blocks of sound waves, and they are used to create different musical notes and tones.
Inverse Sine
The inverse sine function, denoted as arcsin(x), is the inverse of the sine function. It finds the angle x given the sine of x.
arcsin(sin(x)) = x
The inverse sine function has a range of [-π/2, π/2].
Trigonometric Identities
Sine is involved in several important trigonometric identities:
| Identity | Description |
|---|---|
| sin2(x) + cos2(x) = 1 | Pythagorean identity |
| sin(x + y) = sin(x)cos(y) + cos(x)sin(y) | Sum formula |
sin(x
|
Difference formula |
Epilogue: Sine Meaning
In conclusion, sine meaning encompasses a multifaceted concept that finds its echo in countless real-world applications. Its properties, graph, and inverse function provide a powerful toolkit for solving complex problems, while trigonometric identities simplify expressions, revealing the underlying harmony of mathematical relationships.
General Inquiries
What is the mathematical definition of sine?
Sine is defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right triangle.
What are some examples of sine applications?
Sine is used in various fields, including physics (describing wave motion), engineering (analyzing vibrations), and music (determining sound frequencies).
How is the sine function graphed?
The sine function is graphed as a smooth, continuous wave that oscillates between -1 and 1.
What is the inverse sine function?
The inverse sine function, also known as arcsine, is the function that gives the angle whose sine is a given value.